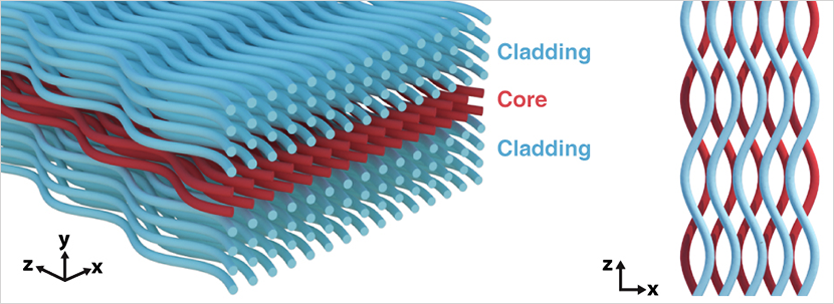
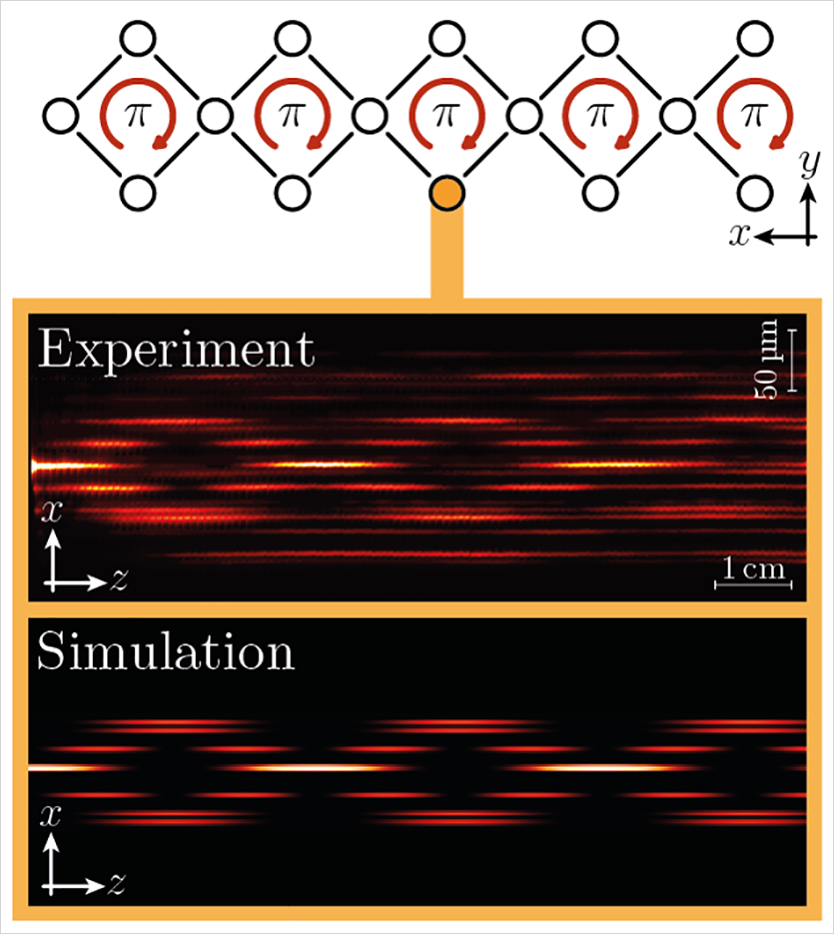
The electric charge quantifies the strength and sign of a particle’s response to an external electromagnetic field. Conversely, these fields cannot exert forces on particles that lack such a charge. Synthetic gauge fields bridge this gap by judiciously employing geometric effects or modulating the properties of the surrounding medium to force uncharged particles to behave as if under the influence of an external field.

In this vein, synthetic gauge fields can endow systems with a wide range of intriguing features beyond what nature has provided them with. As such, the concept of synthetic gauge fields is particularly useful in photonics, where it is instrumental in establishing synthetic magnetic effects in a context that is otherwise notoriously devoid of magnetic responses. Forming the basis for novel wave guiding mechanisms and topological phenomena, synthetic gauge fields in photonics open the door to explore new physics, and, from an applications point of view, facilitate innovative devices by enabling control over light dynamics in new ways, such as a novel conceptual approach for guiding light in integrated photonic structures [Nature Photon. 13, 339 (2019)].

Synthetic gauge fields are a crucial component in our photonic implementations of topological phenomena, such as the first photonic topological insulator [Nature 496, 196 (2013)], the first topological insulator in synthetic dimensions [Nature 567, 356 (2019)], and square-root topological insulators using Aharonov-Bohm cages [Nature Commun. 11, 907 (2020)].

Interestingly, this novel framework allows not only the implementation of electromagnetic gauge fields, but also of non-Abelian structures, known, e.g., from the strong interaction force. Only recently, we were able to realize non-Abelian photonic holonomies [Phys. Rev. Research 1, 033117 (2019)].

Back